
資産運用の際には平均、分散、相関係数などの統計学の知識が必須となります。期待リターン、リスク等の分析が必要なためです。そこで、今回から統計学の基本についてお話しさせていただきたいと思います。今回は「平均」です。
母集団
統計学には「母集団」という言葉があります。「母集団」とは、調査対象となる集合のことを言います。身近な例としては、中学でも高校でも構わないので、1つのクラスを母集団として考えることができます。
その母集団でのテストの点数の調査を考えてみましょう。もちろん、クラスの生徒1人1人のテストの点数全部を調べても良いのですが、それを全部調べたところで、その母集団(クラス)がどのような特性を持つのかを簡単に知れるわけではありません。そこで、その特性を表すものの1つとして「平均」というものがあります。
「平均」というのは、その母集団の代表的な数値の1つであり、テストの点数の場合は、単純に全員のテストの点数の合計を、その人数で割ることによって求めることができます。これによって、代表的な数値、すなわち平均的な数値を求めることができるわけです。
ただ、その平均が必ずしも母集団の代表的な数値として適しているとは限りません。簡単な例として、5人しかいないクラスを考えてみましょう。
ケース1 60、70、80、90、100
ケース2 10、10、10、20、100
それぞれ平均を求めると、
ケース1の場合、
(60+70+80+90+100)÷5=400÷5=80
ケース2の場合
(10+10+10+20+100)÷5=150÷5=30
となります。
ケース1の場合、平均80がこの母集団の代表的数値と言われて違和感はありませんが、ケース2の場合、平均30がこの母集団の代表的数値というと違和感があります。これは、他の人の点数が低い中、1人が100点をとったことにより、平均がこの1人の点数に引っ張られてしまうためです。ですので、平均が必ず母集団の代表的な数値を表すものになるとは限らないわけです。
そのため、平均以外の母集団の代表を表す指標として「中央値」や「最頻値」があります。
「中央値」は、データを小さい順番または大きい順番に並べた場合の真ん中にくる数値のことです。先ほどのケース1、ケース2の場合、
ケース1 60、70、80、90、100
ケース2 10、10、10、20、100
ですので、それぞれ中央値は80、10となるわけです。ケース1では「平均=中央値」となり、ケース2では「平均>中央値」となります。ケース2では、平均30よりも中央値10の方が、この母集団の特性を表す数値として適しているように考えられます。
最頻値
次に「最頻値」ですが、母集団を一定の幅で区切って、その中で最もデータ数が多いところを「最頻値」とします。簡単な例として、テストの点数を10点の幅で区切って集計したとします。
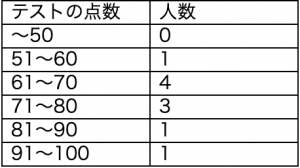
この場合、点数が「61~70」が最も多いわけでここが「最頻値」となります。「61~70」と幅で持っていますので、この場合は、その中の代表的な数値として「65」としたりするわけです。
以上のとおり、統計学の初歩的な部分としては、まず母集団の特性を表す数値を探すことから始めます。その最たる例として「平均」などがあるわけです。
ただ、平均が等しい2つの母集団があったとしても、実際には、2つの母集団の特性は大きく異なったりする場合もあるわけです。






















